Generating π in CL (faster)

Thanks to metacircular for pointing out that (floor (/ x y)) can be written as (floor x y) while avoiding
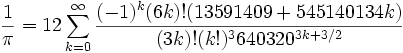
the intermediate rational.

(defun machin-pi (digits)
  "Calculates PI digits using fixed point arithmetic and Machin's formula with double recursion"
  (labels
      ((arccot-minus (xsq n xpower)
         (let ((term (floor xpower n)))
           (if (= term 0)
               0
               (- (arccot-plus xsq (+ n 2) (floor xpower xsq))
                  term))))
       (arccot-plus (xsq n xpower)
         (let ((term (floor (/ xpower n))))
           (if (= term 0)
               0
               (+ (arccot-minus xsq (+ n 2) (floor xpower xsq))
                  term))))
       (arccot (x unity)
         (let ((xpower (floor (/ unity x))))
           (arccot-plus (* x x) 1 xpower))))
    (let* ((unity (expt 10 (+ digits 10)))
           (thispi (* 4 (- (* 4 (arccot 5 unity)) (arccot 239 unity)))))
      (floor thispi (expt 10 10)))))

The first 10000 digits again.

* (time (machin-pi 10000))
Evaluation took:
  0.662 seconds of real time
  0.634038 seconds of total run time (0.495454 user, 0.138584 system)
  [ Run times consist of 0.233 seconds GC time, and 0.402 seconds non-GC time. ]
  95.77% CPU
  1,491,387,858 processor cycles
  109,530,592 bytes consed
31415926535897932384626433832795028841971693993751058209749445923078164062862089 ...

Algorithmic optimizations would take us much further. For example the Gauss–Legendre or Salamin–Brent formula.
Then there is the fastest known(at the turn of the millenium), Chudnovsky’s formula :